Trees (Part 1)

Introduction to Trees

Trees are one of the fundamental data structures in computer science.
Trees are a specific type of graph, but much simpler.
They are constructed so as to retrieve information rapidly.
Typical search times for trees are O(lg N) (Think of the ability to do binary search on a linked list.)

A generic tree:

Terminology

Trees consist of vertices and edges.
Vertex - An object that carries associated information [1, 2, 3]
- node
Edge - A connection between two vertices. A link from one node to another. [a, b, c]
Child/Parent - If either the right or left link of A is a link to B, then B is a child of A and A is a parent of B.
- 4, 5, and 6 are children of 2; 2 is the parent of 4, 5, and 6
Sibling - Nodes that have the same parent. [2, 3] have the same parent.
A node that has no parent is called the root of a tree [1]. There is only one root in any given tree.
Path - A list of vertices [1-2-4]
Leaf - A node with no children [4, 7]
- external node
- terminal node
- terminal
Non-leaf - A node with at least one child [1, 2, 5]
- internal node
- non-terminal node
- non-terminal
Depth (or height) - the length of the longest path from the root to a leaf. [1, 2, 5, 7 = 3]
- The number of edges in the path is the length. (Or, number of nodes - 1)
- A tree consisting of 1 node (the root), has a height of 0.
Subtree - Any given node, with all of its descendants (children). [5, 7, 8] is a subtree, 5 is the root.
Trees can be ordered or unordered
- Ordered trees specify the order of the children (examples: parse tree, binary search tree)
- Unordered trees place no criteria on the ordering of the children (example: file system directories)
M-ary tree - A tree which must have a specific number of children in a specific order.
- Binary tree - An M-ary tree where
  - all internal nodes have one or two children
  - all external nodes (leaves) have no children
  - the two children may be sorted and are called the left child and right child
- B-tree - An M-ary tree where
  - all internal nodes have between N and N/2 children (where N is generally several hundred)
  - the children are sorted according to some sort order or key

Basic Properties

A node has at most one edge leading to it.
- Each node has exactly one parent, except the root which has no parent.
There is at most one path from one node to any other node.
- If there are multiple paths, it's a graph not a tree.
There is exactly one path from the root to any leaf.

Other Properties

The level of a given node in a tree is defined recursively as:

0                   if node is a root
level(parent) + 1   if node is a child of parent

Two interpretations of height (or depth):

1. The height of a tree is the length of the longest path from the root to a leaf.
2. The height is the maximum of the levels of the tree's nodes.

These are all trees.

This is not a tree. (Y has 2 parents)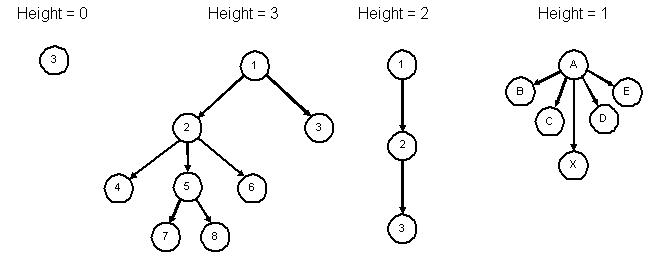

Don't confuse the size of a tree with the height of a tree. The size is simply the number (count) of nodes in the tree.

Binary Trees

A binary tree is a collection of nodes such that:

There are two distinct types of nodes: internal and external
An internal node contains exactly two links, left and right
The two links are disjoint binary trees (they have no nodes in common)
One or both links can be NULL (an empty tree)

A binary tree with N internal nodes has N + 1 external nodes (some may be empty/NULL)
A binary tree with N internal nodes has 2N links
Representing binary trees with diagrams: sometimes an empty box is used to indicate an empty child (empty subtree). The squares are external nodes (leaves) and the circles are internal nodes. These diagrams are referred to as extended binary trees:

A binary tree An extended binary tree
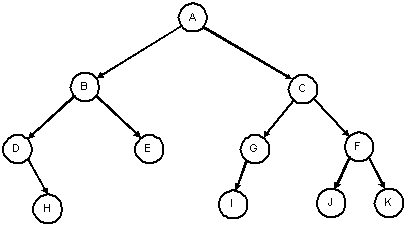
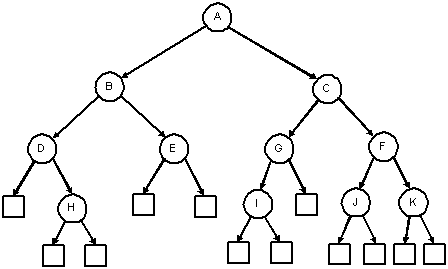
A balanced binary tree (height-balanced) is a tree where for each node the depth of the left and right subtrees differ by no more than 1.

A balanced binary tree An unbalanced binary tree

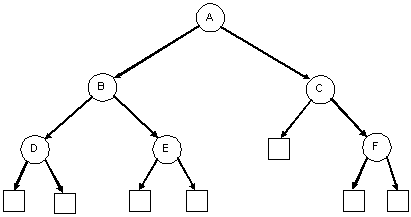
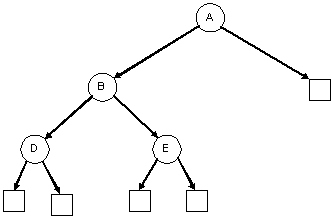
A degenerate binary tree A balanced binary tree (it's also a complete binary tree)

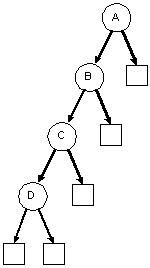
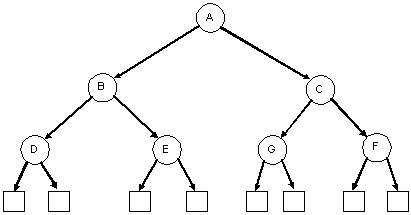
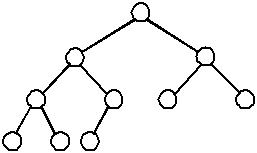
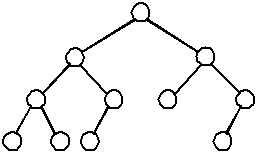
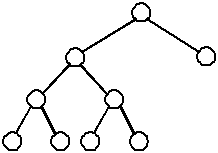
A complete binary tree is similar to a balanced binary tree except that all of the leaves must be placed as far to the left as possible. (The leaves must be "filled-in" from left to right, one level at a time.)

A complete binary tree An incomplete binary tree An incomplete binary tree

Realize that the two links in a binary tree are not quite the same as the two links in a doubly linked list:
- Trees have a left and right link.
- Lists have a previous and next link.
- Both imply ordering, but a different kind of ordering.
- Implementation wise, the nodes can be structurally equivalent.

struct ListNode
{
  ListNode *next;
  ListNode *prev;
  Data *data;
};

struct TreeNode
{
  TreeNode *left;
  TreeNode *right;
  Data *data;
};

Tree:

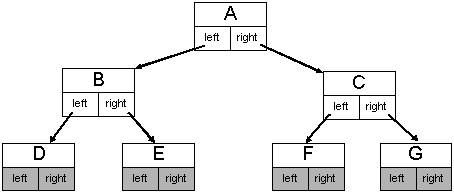
Linked list:

Self-check What is a binary tree? What is a balanced tree? What is a complete tree?

Traversing Binary Trees

Because trees are a recursive data structure, recursive algorithms are quite appropriate. In some cases, iterative (non-recursive) algorithms can be significantly more complicated.

How would you traverse a linked list recursively? (How many ways can you traverse it?) Reminder: Traversing linked-list recursively.

Recursive algorithm Recursive algorithm with base case

Preorder traversal

Visit the node
Traverse (pre-order) the left subtree
Traverse (pre-order) the right subtree

Inorder traversal

Traverse (in-order) the left subtree
Visit the node
Traverse (in-order) the right subtree

Postorder traversal

Traverse (post-order) the left subtree
Traverse (post-order) the right subtree
Visit the node

Preorder traversal
If node is not empty

Visit the node
Traverse (pre-order) the left subtree
Traverse (pre-order) the right subtree

Inorder traversal
If node is not empty

Traverse (in-order) the left subtree
Visit the node
Traverse (in-order) the right subtree

Postorder traversal
If node is not empty

Traverse (post-order) the left subtree
Traverse (post-order) the right subtree
Visit the node

Recursive algorithm		Recursive algorithm with base case
Preorder traversal Visit the node Traverse (pre-order) the left subtree Traverse (pre-order) the right subtree Inorder traversal Traverse (in-order) the left subtree Visit the node Traverse (in-order) the right subtree Postorder traversal Traverse (post-order) the left subtree Traverse (post-order) the right subtree Visit the node		Preorder traversal If node is not empty Visit the node Traverse (pre-order) the left subtree Traverse (pre-order) the right subtree Inorder traversal If node is not empty Traverse (in-order) the left subtree Visit the node Traverse (in-order) the right subtree Postorder traversal If node is not empty Traverse (post-order) the left subtree Traverse (post-order) the right subtree Visit the node

Given these binary trees:

assume that visiting a node means printing the letter of the node. The result of the traversing the first tree is A in all 3 cases.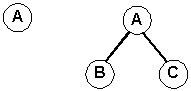

For the second tree, we have:

Preorder traversal: ABC (visit, traverse left, traverse right)
Inorder traversal: BAC (traverse left, visit, traverse right)
Postorder traversal: BCA (traverse left, traverse right, visit)

Self-check Perform the three different traversals on the tree below.

Assuming that visiting a node means printing the letter of the node, what is the output for

a preorder traversal?
an inorder traversal?
a postorder traversal?

A (binary) tree showing the relationships between musical notes:

An example of an expression tree: (order is important)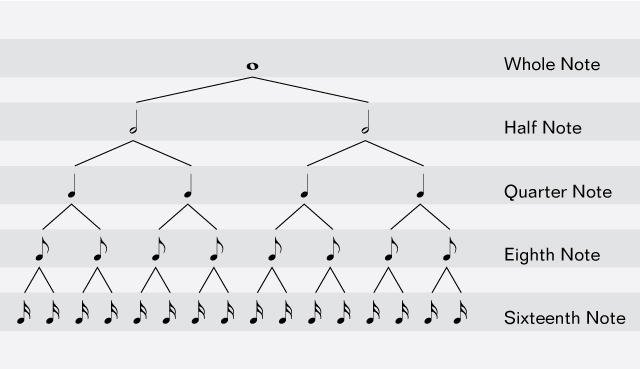

Self-check What kind of traversal would we use to evaluate the expression tree?

Implementing Tree Algorithms

Assume we have these definitions:

struct Node
{
  Node *left;
  Node *right;
  int data;
};

Node *MakeNode(int Data)
{
  Node *node = new Node;
  node->data = Data;
  node->left = 0;
  node->right = 0;
  return node;
}

void FreeNode(Node *node)
{
  delete node;
}

typedef Node* Tree;

We can construct binary trees by providing a height for the final tree. Assume that the data items are the letters A, B, C, D, etc. added in that order.

Linked list examples

int Count = 0;

Tree BuildBinTreePre(int height)
{
  if (height == -1)
    return 0;

  Node *node = MakeNode('A' + Count++);      // build the node
  node->left = BuildBinTreePre(height - 1);  // build the left tree
  node->right = BuildBinTreePre(height - 1); // build the right tree
  return node;
}

void main()
{
  Tree t = BuildBinTreePre(1);
}

This results in a tree that looks like this:

  A
 / \
B   C

The name of the function tells us in which order this tree has been built (preorder).

How would we construct these trees?

  B         C
 / \       / \
A   C     A   B

Notice when the node/subtrees are being constructed:

Tree BuildBinTreeIn(int height)
{
  if (height == -1)
    return 0;

  Node *node = new Node;
  node->left = BuildBinTreeIn(height - 1);  // build left subtree
  node->data = 'A' + Count++;               // build node
  node->right = BuildBinTreeIn(height - 1); // build right subtree
  return node;
}

Tree BuildBinTreePost(int height)
{
  if (height == -1)
    return 0;

  Node *node = new Node;
  node->left = BuildBinTreePost(height - 1);  // build left subtree
  node->right = BuildBinTreePost(height - 1); // build right subtree
  node->data = 'A' + Count++;                 // build node
  return node;
}

Self-check: Suppose you used these functions to create a tree with height of 2. This would require 7 nodes and use the letters: ABCDEFG. What would the trees look like using: BuildBinTreePre? BuildBinTreeIn? BuildBinTreePost?

More Tree Algorithms

State the recursive algorithms for finding:

the number of nodes in a tree
the height of a tree

Definitions and sample implementations:

Finding the number of nodes in a tree.

0                         if the tree is empty
1 +                       if tree is not empty
nodes in left subtree +
nodes in right subtree

int NodeCount(Tree tree)
{
  if (tree == 0)
    return 0;
  else
    return 1 + NodeCount(tree->left) + NodeCount(tree->right);
}

Finding the height of a tree.

-1                            if the tree is empty (Definition)
 1 + height of left subtree   if height of left subtree > height of right subtree
 1 + height of right subtree  otherwise

Implementation #1: (naive, from the definition)

int Height(Tree tree)
{
  if (tree == 0)
    return -1;

  if (Height(tree->left) > Height(tree->right))
    return Height(tree->left) + 1;
  else
    return Height(tree->right) + 1;
}

Implementation #2:

int Height(Tree tree)
{
  if (tree == 0)
    return -1;

  int lh = Height(tree->left);
  int rh = Height(tree->right);

  if (lh > rh)
    return lh + 1;
  else
    return rh + 1;
}

Implementation #3:

int Height(Tree tree)
{
  if (tree == 0)
    return -1;
  else
    return (1 + Max(Height(tree->left), Height(tree->right)));
}

Assume that "visting" a node simply means printing out the value of the data element:

void VisitNode(Tree tree)
{
  cout << tree->data << endl;
}

We can implement three traversal algorithms like this:


Implementation #1 Implementation #2


void TraversePreOrder(Tree tree)
{
  if (tree == 0)
    return;

  VisitNode(tree);
  TraversePreOrder(tree->left);
  TraversePreOrder(tree->right);
}

void TraverseInOrder(Tree tree)
{
  if (tree == 0)
    return;

  TraverseInOrder(tree->left);
  VisitNode(tree);
  TraverseInOrder(tree->right);
}

void TraversePostOrder(Tree tree)
{
  if (tree == 0)
    return;

  TraversePostOrder(tree->left);
  TraversePostOrder(tree->right);
  VisitNode(tree);
}






void TraversePreOrder(Tree tree)
{
  if (tree)
  {
    VisitNode(tree);
    TraversePreOrder(tree->left);
    TraversePreOrder(tree->right);
  }
}

void TraverseInOrder(Tree tree)
{
  if (tree)
  {
    TraverseInOrder(tree->left);
    VisitNode(tree);
    TraverseInOrder(tree->right);
  }
}

void TraversePostOrder(Tree tree)
{
  if (tree)
  {
    TraversePostOrder(tree->left);
    TraversePostOrder(tree->right);
    VisitNode(tree);
  }
}

Implementation #1		Implementation #2
void TraversePreOrder(Tree tree) { if (tree == 0) return; VisitNode(tree); TraversePreOrder(tree->left); TraversePreOrder(tree->right); } void TraverseInOrder(Tree tree) { if (tree == 0) return; TraverseInOrder(tree->left); VisitNode(tree); TraverseInOrder(tree->right); } void TraversePostOrder(Tree tree) { if (tree == 0) return; TraversePostOrder(tree->left); TraversePostOrder(tree->right); VisitNode(tree); }		void TraversePreOrder(Tree tree) { if (tree) { VisitNode(tree); TraversePreOrder(tree->left); TraversePreOrder(tree->right); } } void TraverseInOrder(Tree tree) { if (tree) { TraverseInOrder(tree->left); VisitNode(tree); TraverseInOrder(tree->right); } } void TraversePostOrder(Tree tree) { if (tree) { TraversePostOrder(tree->left); TraversePostOrder(tree->right); VisitNode(tree); } }

Self-check Using the implementations above, what is the complexity for each of these traversal orders? In other words, how many nodes are visited? (How many times is each node accessed?)

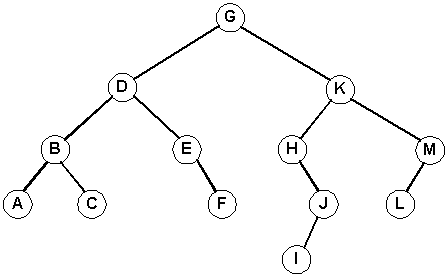
Level-Order Traversal

Traversing all nodes on level 0, from left to right, then all nodes on level 1 (left to right), then nodes on level 2 (left to right), etc. is level-order traversal.

So, a level-order traversal of this tree:

Modula-2 ©2008

will result in the nodes being visited in this order:

G D K B E H M A C F J L I

Traversing in level-order really isn't any more complicated by definition:

The recursive definition:

If the level being visited is:   0    Visit the node

If the level being visited is: > 0    Traverse the left subtree in level order
                                      Traverse the right subtree in level order

Sample code: Note the use of a helper recursive function.

 1. void TraverseLevelOrder(Tree tree)
 2. {
 3.  int height = Height(tree);
 4.  for (int i = 0; i <= height; i++)
 5.    TraverseLevelOrder2(tree, i);
 6. }

 7. void TraverseLevelOrder2(Tree tree, int level)
 8. {
 9.   if (level == 0)
10.     VisitNode(tree);
11.   else
12.   {
13.     TraverseLevelOrder2(tree->left, level - 1);
14.     TraverseLevelOrder2(tree->right, level - 1);
15.   }
16. }

Using the implementations above, what is the complexity for level-order traversal? In other words, how many nodes are accessed? (How many times is each node accessed?)

Details of the TraverseLevelOrder2 function above:

  Level    Nodes at level N   Nodes in tree    Node Accesses
------------------------------------------------------------
    0             1                 1                  1
    1             2                 3                  4
    2             4                 7                 11
    3             8                15                 26
    4            16                31                 57
    5            32                63                120
    6            64               127                247
    7           128               255                502
    8           256               511               1013
    9           512              1023               2036
   10          1024              2047               4083
   11          2048              4095               8178
   12          4096              8191              16369
   13          8192             16383              32752
   14         16384             32767              65519
   15         32768             65535             131054
   16         65536            131071             262125
   17        131072            262143             524268
   18        262144            524287            1048555
   19        524288           1048575            2097130

Self Check: Modify the algorithm above so it prints the nodes in reverse level-order:

I L J F C A M H E B K D G

Level-order traversal using a queue

Pseudocode
If the tree isn't empty Push the node onto the Queue While the Queue isn't empty Pop a node from the Queue Visit the node If the node's left child is not NULL Push the left child onto the Queue If the node's right child is not NULL Push the right child onto the Queue End While End If

Pseudocode


If the tree isn't empty
  Push the node onto the Queue
  While the Queue isn't empty
    Pop a node from the Queue
    Visit the node
    If the node's left child is not NULL
      Push the left child onto the Queue
    If the node's right child is not NULL
      Push the right child onto the Queue
  End While
End If

What is the complexity for this level-order traversal? How does the implementation of the Queue data structure affect the complexity?

Self Check: Implement a function similar to TraverseLevelOrder that uses a queue as an auxiliary data structure. The function won't be recursive.

Self Check: Implement a function similar to TraverseLevelOrder that uses a stack as an auxiliary data structure. The function won't be recursive. What order is this traversal?

Binary Search Trees

Definition

A binary search tree (BST) is a binary tree in which the values in the left subtree of a node are all less than the value in the node, and the values in the right subtree of a node are all greater than the value of the node. The subtrees of a binary search tree must themselves be binary search trees. (Recursive)

Note that under this definition, a BST never contains duplicate nodes.

Some operations for BSTs:

InsertItem
DeleteItem
ItemExists
Traverse (Pre, In, Post)
Count
Height

Notes:

Count and Height (Depth) are straight-forward as above.
The Traverse routines are also as above.
ItemExists and InsertItem are also trivial:

Using the same definitions from above:

struct Node { Node *left; Node *right; int data; };

Node *MakeNode(int Data) { Node *node = new Node; node->data = Data; node->left = 0; node->right = 0; return node; }

void FreeNode(Node *node) { delete node; } typedef Node* Tree;

As always

State the recursive algorithm (in English) for finding an item in a BST.
State the recursive algorithm (in English) for inserting an item into a BST.
Call these two functions ItemExists and InsertItem.
What are the parameters to these functions?

Sample code for finding an item in a BST:

bool ItemExists(Tree tree, int Data) { if (tree == 0) return false; else if (Data == tree->data) return true; else if (Data < tree->data) return ItemExists(tree->left, Data); else return ItemExists(tree->right, Data); }

Sample code for inserting an item into a BST:

void InsertItem(Tree &tree, int Data)
{
  if (tree == 0)
    tree = MakeNode(Data);
  else if (Data < tree->data)
    InsertItem(tree->left, Data);
  else if (Data > tree->data)
    InsertItem(tree->right, Data);
  else
    cout << "Error, duplicate item" << endl;
}

Notice that the inserted item will always be placed as a leaf node at the bottom of the tree. You never insert a node somewhere in the "middle" of the tree.

Self Check: Create a tree using these values (in this order): 12, 22, 8, 19, 10, 9, 20, 4, 2, 6

What is the height of the resulting tree? What can you say about the tree? (Is it balanced? Is it complete? If it is unbalanced, which nodes are out of balance?)

Self Check: Create a tree using the same values but in this order: 2, 4, 6, 10, 8, 22, 12, 9, 19, 20

What is the height of the resulting tree? What can you say about the tree? (Is it balanced? Is it complete? If it is unbalanced, which nodes are out of balance?)

Diagrams of the results.

Self Check: What is the worst case time complexity for searching a BST? Best? What causes the best/worst cases?

Search Times

BST algorithms are highly dependent on the input data.
One solution is to balance the tree.
Balancing BSTs can be expensive and the algorithms are more complex than what we've seen so far.
- Balancing a tree is somewhat analagous to sorting a linked-list.
- Trees have the same benefit as lists of not having to copy the data (just change pointers).
One type of balanced tree is the AVL tree (Two Russian Mathematicians, Adel'son-Vel'skii and Landis). More on this later.

Self Check: Given a BST with 10 nodes, what is the maximum and minimum height of the tree? Suppose the BST had 20 nodes?

Self Check: Given a BST of height 2, what is the maximum and minimum number of leaves in the tree? What if the BST had a height of 3?

Deleting A Node

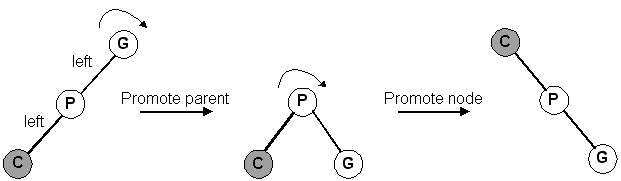
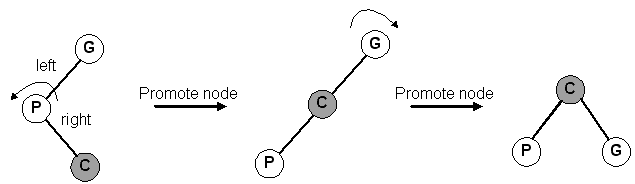
The caveat of deleting a node is that, after deletion, the tree must still be a BST. Using this tree as an example:

There are four cases to consider:

The node to be deleted is a leaf. (Nodes: A C F I L)
This is trivial. Set the parent's pointer to this node to NULL.
The node to be deleted has an empty left child but non-empty right child. (Nodes: E H)
Replace the deleted node with its right child. Note that this case can be combined with Case #1 by "promoting" the right child. This works even if the right child is NULL.
The node to be deleted has an empty right child but non-empty left child. (Nodes: J M)
Similar to #2. Promote the left child.
The node to be deleted has both children non-empty. (Nodes: B D G K)
- Replace the data in the deleted node with its predecessor under inorder traversal.
- Delete the node that held the predecessor.
- The predecessor will be the rightmost node in the left subtree of the deleted node.
- In the diagram, this is A if B is deleted, C if D is deleted, F if G is deleted, and J if K is deleted.

Notes about Case #4

We are replacing the data in the node, not the node itself.

This is an implementation detail as the node can be re-used if done properly.

Because the predecessor comes from the left subtree:

it must be less than everything in the right subtree
it is an inorder predecessor so it must be greater than everything else in the left subtree

The recursive deletion of the predecessor's node will find the node in one of the simpler cases.

To implement the DeleteItem function, we use a helper function called FindPredecessor, which simply finds the inorder predecessor for a given node.

void DeleteItem(Tree &tree, int Data) { if (tree == 0) return; else if (Data < tree->data) DeleteItem(tree->left, Data); else if (Data > tree->data) DeleteItem(tree->right, Data); else // (Data == tree->data) { if (tree->left == 0) { Tree temp = tree; tree = tree->right; FreeNode(temp); } else if (tree->right == 0) { Tree temp = tree; tree = tree->left; FreeNode(temp); } else { Tree pred = 0; FindPredecessor(tree, pred); tree->data = pred->data; DeleteItem(tree->left, tree->data); } } } void FindPredecessor(Tree tree, Tree &predecessor) { predecessor = tree->left; while (predecessor->right != 0) predecessor = predecessor->right; }

Modula-2 ©2008

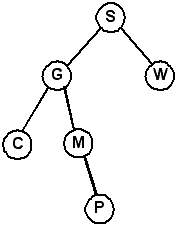
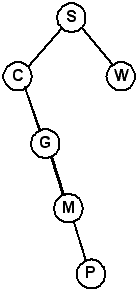
Self Check: What is the resulting tree from deleting the root node (G) in the tree above? What does the tree look like if you delete K from the tree?

Rotating Nodes

Rotation is a fundamental technique that is performed on BSTs.
There are two types of rotations: left and right.
Rotating a node is the same as promoting one of the node's children.

Promoting a child means that it will take the place of its parent.
Rotate left means promote the right child.
Rotate right means promote the left child.
You can't rotate if the necessary child is missing (NULL), which means you can't promote an empty child.

So, promoting a node is the same as rotating around the node's parent. (There is no direction, promotion is unambiguous.)
You can rotate about any node that has the necessary child.

Note: An important property of rotation is that after the rotation, the sort order is preserved. This is important, because the resulting tree must still be a BST.

Rotate right about the root, S. (Same as promoting the left child, M)

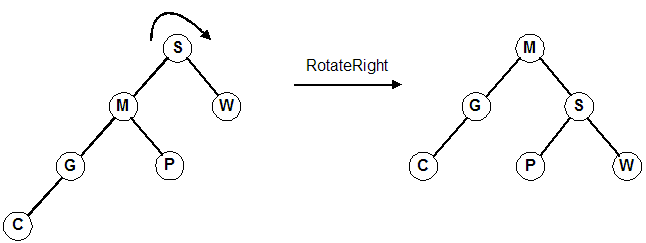
Rotate left twice about the root. (Far right diagram) First rotate about 1, then rotate about 3. (Same as promoting 3 and then promoting 6)

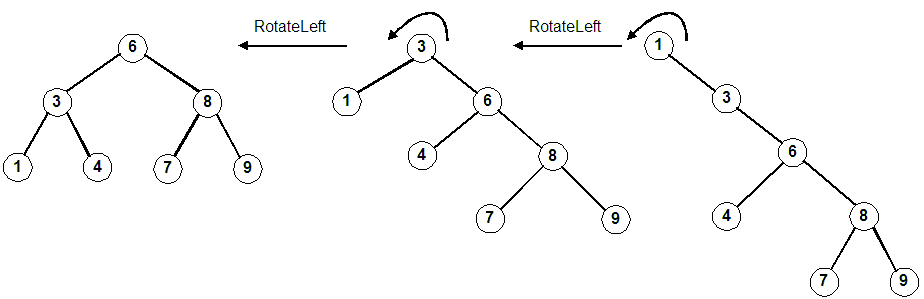
Using the defintions above. Note the parameter to each function is a reference to a pointer.

Rotating a tree right	Rotating a tree left
void RotateRight(Tree &tree) { Tree temp = tree; tree = tree->left; temp->left = tree->right; tree->right = temp; }	void RotateLeft(Tree &tree) { Tree temp = tree; tree = tree->right; temp->right = tree->left; tree->left = temp; }

Rotating a tree right

Rotating a tree left

void RotateRight(Tree &tree)
{
  Tree temp = tree;
  tree = tree->left;
  temp->left = tree->right;       
  tree->right = temp;
}

void RotateLeft(Tree &tree)
{
  Tree temp = tree;
  tree = tree->right;
  temp->right = tree->left;
  tree->left = temp;
}

Follow the four lines of code in this example. We are rotating right about S (promoting M).

1. temp = Tree;              // temp ===> S
2. tree = temp->left;        // tree ===> M
3. temp->left = tree->right; // temp->left ===> P
4. tree->right = temp;       // tree->right ===> S

Adjusting the diagram: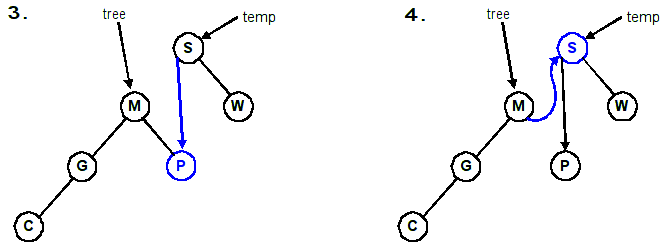

You can easily see why we passed a reference (or pointer) to the root of the tree. If you just pass the pointer itself (by value), after the rotation tree still points at node S, which is wrong. Keep this in mind when you are implementing the tree functions.

Note that these four trees below all contain the same data.

One Two Three Four

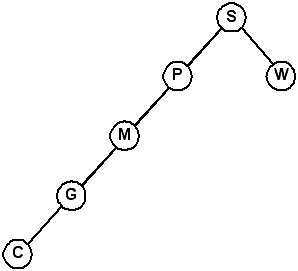
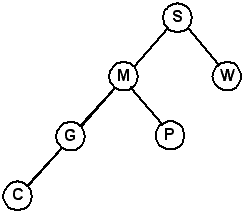
Can you explain why there are four different representations for the same data?

Self Check: What is the resulting tree from rotating left about the root node (G) in the tree below? How about rotating right about the root? Rotating left about a node means promoting the node's right child. Rotating right about a node means promoting the node's left child.

Self Check: After rotating right about G above, the tree is unbalanced because at least one node is unbalanced. Specifically, which nodes are unbalanced?

Self Check: Insert the letters: P I N K F L O Y D E R S into a BST. What is the height of the tree? The tree is NOT balanced. Which nodes in the tree are unbalanced? Rotate about the root (P) node. Now what is the height of the tree? Which nodes are unbalanced now? Finally, delete node P from the original tree.

Self Check: Insert the letters: K E Y B O A R D I S T into a BST. What is the height of the tree? The tree is NOT balanced. Which nodes in the tree are unbalanced? Rotate about the root (K) node. Now what is the height of the tree? Which nodes are unbalanced now? Finally, delete node E from the rotated tree.

Self Check: Insert the letters: K E Y B O A R D I S T into a BST. What is the sequence of letters when doing a Pre-order traversal? An In-order traversal? A Post-order traversal?

Splay Trees

Invented by D.D. Sleator and R.E. Tarjan in 1985.

Most of the time, we don't make any assumptions about the data.
Usually assume equal distribution of data and random values.
Non-random data can lead to worst-case situations (building a BST from already-sorted data).
Non-uniform distribution of data can also lead to worst-case situations.
If we know how the data is distributed, we can choose better data structures.

A splay tree uses this knowledge to an advantage.

A splay tree is a binary search tree.
Newly inserted items are propagated (promoted) to the root.
This propagation occurs when writing (inserting) and reading (accessing) an item.
We call this propagation of a node splaying.

The idea behind splay trees is that frequently accessed data is always near the top.

Splay trees are not guaranteed to be balanced
Worst-case is not guaranteed to be "good"
Average time may be excellent (this may be more important than worst case)
Algorithms for splaying a node are simple (only require rotation)
The algorithm is a variation of the more general BST root insertion

Splaying algorithm

We want to splay a node two levels at a time.
This means we want to promote the node to the position of its grandparent (parent's parent)
The algorithm depends on the node's orientation to its grandparent (1 of 4 orientations)
1. left-left, promote the parent, promote the node
2. left-right, promote the node, promote the node (node is promoted twice)
3. right-right, promote the parent, promote the node
4. right-left, promote the node, promote the node (node is promoted twice)

Promoting a node simply means rotating about the node's parent (which we've done). Promoting a node doesn't require you to specify left or right. The direction is implied.

If node is a right-child, rotate parent LEFT
If node is a left-child, rotate parent RIGHT

Left-Left orientation (zig-zig)

Left-Right orientation (zig-zag)

Right-Right orientation (zig-zig)

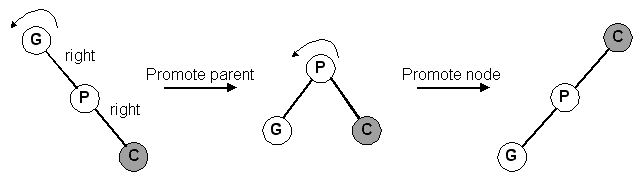
Right-Left orientation (zig-zag)

We continue to promote until we reach the root.
The "special case" is if our parent is the root.
If the parent is the root, simply perform a rotation to bring the node to the root.

In the example below, we want to splay node C to the root.

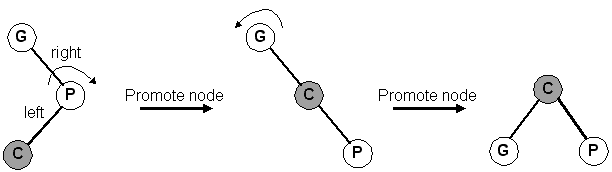
Our orientation with our grandparent is left-right at first:

Now, our orientation with our grandparent is left-left: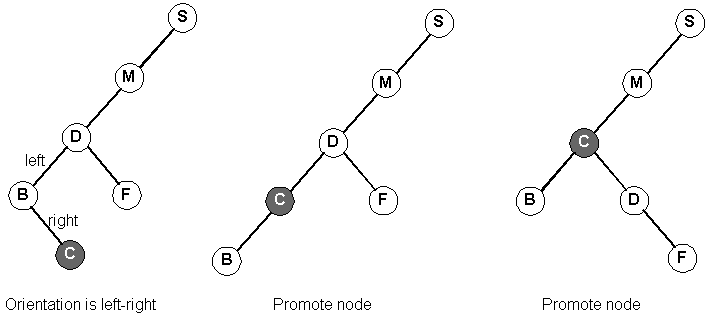

The result of splaying F to the root: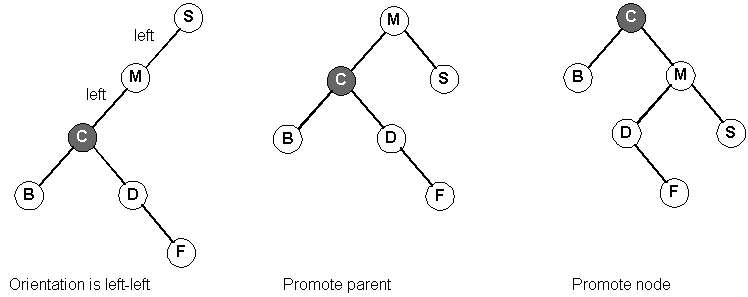

Additional Notes: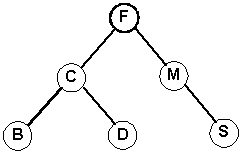

Good amortized performance: The average cost is efficient.
Acts sort of like a built-in caching mechanism.
Works well with non-uniform access patterns over a small working set.

You may have millions of nodes but are repeatedly accessing the same 50 or so nodes.

Simple to implement.

Expression Trees

Expression trees are like binary trees, but they are not "sorted" in the usual way.

Given this expression:

(7 + 5) * (3 + 4) - (4 * (9 - 2))

The result after evaluation is 56. The tree that represents it looks like this:

Operators are always internal nodes and operands are always external (leaf) nodes.

(7 + 5) * (3 + 4) - (4 * (9 - 2))
        ^         ^    ^     
        |         |    |
        |         |    |
    root of     root  root of
  left subtree        right subtree

Evaluating the tree gives the same result. Evaluating an expression tree simply means reducing each subtree by post-order traversal. Why post-order?

Self-Check: Perform a post-order traversal on the expression tree above. This will create a postfix expression. Using the stack method from here, evaluate it and verify that you get the value 56.

Grammar

A simple definition for the grammar, or language, that defines an expression looks something like this:

<expression> ::= <term> { <addop> <term> }
<term>       ::= <factor> { <mulop> <factor> }
<factor>     ::= ( <expression> ) | <identifier> | <literal>
<addop>      ::= + | -
<mulop>      ::= * | /
<identifier> ::= a | b | c | ... | z | A | B | C | ... | Z
<literal>    ::= 0 | 1 | 2 | ... | 9

Note that the grammar is (indirectly) recursive. The vertical bars are read as "OR", and the curly braces means that the item inside can be repeated 0 or more times.

Our "language" consists of the following tokens:

Valid tokens: ()+-*/abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789

Examples:

 Valid expressions: A, B, 1, A + 2, A + B, A * (B), A * (B - 2), (1)
Invalid constructs: AB, 3A, 123, A(3), A + (), A * -3

Given any infix valid expression within the language, we can evaluate or reduce the expression in a two-step process:

Construct a parse tree from the infix expression.
Simplify the parse tree by evaluating sub-trees (sub-expressions).

Step 1: Pseudocode for Parsing

<expression> ::= <term> { <addop> <term> }
<term>       ::= <factor> { <mulop> <factor> }
<factor>     ::= ( <expression> ) | <identifier> | <literal>


MakeExpression(Tree)
 1  Make a term, setting Tree to point to it

 2  while the next token is '+' or '-'
 3    Make an operator node, setting left child to Tree and right to NULL. (Tree points to new node)
 4    Get the next token.
 5    Make a term, setting the right child of Tree to point to it.
 6  end while
End MakeExpression

MakeTerm(Tree)
 7  Make a factor, setting Tree to point to it

 8  while the next token is '*' or '/'
 9    Make an operator node, setting left child to Tree and right to NULL. (Tree points to new node)
10    Get the next token.
11    Make a factor, setting the right child of Tree to point to it.
12  end while
End MakeTerm

MakeFactor(Tree)
13  if current token is '(', then
14    Get the next token
15    Make an expression, setting Tree to point to it
16  else if current token is an IDENTIFIER
17    Make an identifier node, set Tree to point to it, set left/right children to NULL.
18  else if current token is a LITERAL
19    Make a literal node, set Tree to point to it, set left/right children to NULL.
20  end if

21  Get the next token
End MakeFactor


GetNextToken
  while whitespace
    Increment CurrentPosition
  end while

  CurrentToken = Expression[CurrentPosition]

  Increment CurrentPosition
End GetNextToken

<expression> ::= <term> { <addop> <term> }
<term>       ::= <factor> { <mulop> <factor> }
<factor>     ::= ( <expression> ) | <identifier> | <literal>

Definitions

Some implementations

Diagrams for the expression: A + B (All addresses are arbitrary, but represent the order the nodes were created.)

Make an IDENTIFIER (EXPRESSION → TERM → FACTOR → IDENTIFIER) node and set Tree to point to this term.
Make an OPERATOR node, set left child to Tree and right child to NULL. (Tree now points to this new operator node)
Make an IDENTIFIER (EXPRESSION → TERM → FACTOR → IDENTIFIER) node and set right child of Tree to point to this term.

A A + A + B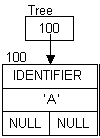

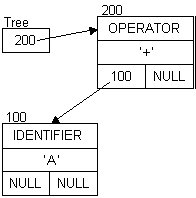
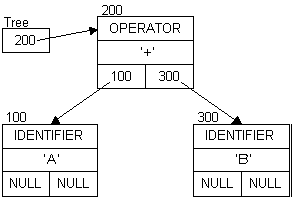
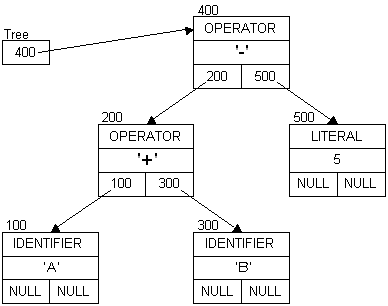
Extending the expression to: A + B - 5

Make an OPERATOR node, set left child to Tree (from above) and right child to NULL. (Tree now points to this new operator node)
Make a LITERAL (EXPRESSION → TERM → FACTOR → LITERAL) node and set right child of Tree to point to this term.

A + B - A + B - 5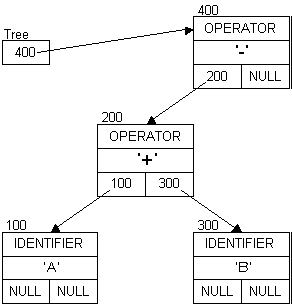

Diagrams for the expression: A + B * C

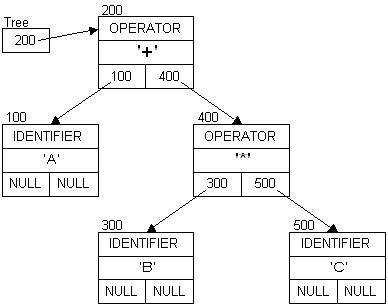
A + B as before:

Adding: * C

Make an OPERATOR node, set left child to Tree (from above, tree is the right pointer of '+') and right child to NULL. (Tree now points to this new operator node)
Make a LITERAL (TERM → FACTOR → LITERAL) node and set right child of Tree to point to this term.

A + B * A + B * C

Step 2: Simplifying the Parse Tree

Algorithm to recursively simplify a tree:

Recursively simplify left subtree
Recursively simplify right subtree
Simplfy the node (perform the arithmetic, no recursion)

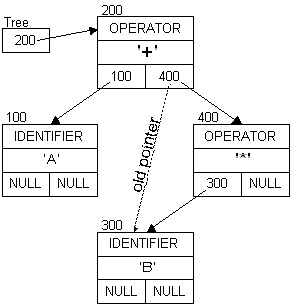
Some simplification examples:

4 * (2 + 3) → 20      A * (2 + 3) → A * 5      A * (3 - 4 + 1) + B → B        A + 2 * 3 → A + 6

Simplification Rules:

Condition Action

Both children are LITERAL Evaluate the expression and promote the result to the node that contained the operator. 0 / 0 → (exception)

The left child is a LITERAL and the right child is an IDENTIFIER or OPERATOR (expression). If expression is one of these forms, it can be simplified and the result promoted:
0 + E → E 1 * E → E 0 * E → 0 0 / E → 0

The right child is a LITERAL and the left child is an IDENTIFIER or OPERATOR (expression). If expression is one of these forms, it can be simplified and the result promoted:
E + 0 → E E - 0 → E E * 0 → 0 E * 1 → E E / 1 → E E / 0 → (exception)

Both children are IDENTIFIER. If expression is one of these forms, it can be simplified and the result promoted:
I - I → 0 I / I → 1

Condition	Action
Both children are LITERAL	Evaluate the expression and promote the result to the node that contained the operator. 0 / 0 → (exception)
The left child is a LITERAL and the right child is an IDENTIFIER or OPERATOR (expression).	If expression is one of these forms, it can be simplified and the result promoted: 0 + E → E 1 * E → E 0 * E → 0 0 / E → 0
The right child is a LITERAL and the left child is an IDENTIFIER or OPERATOR (expression).	If expression is one of these forms, it can be simplified and the result promoted: E + 0 → E E - 0 → E E * 0 → 0 E * 1 → E E / 1 → E E / 0 → (exception)
Both children are IDENTIFIER.	If expression is one of these forms, it can be simplified and the result promoted: I - I → 0 I / I → 1

Example of the form: E - 0 → E

a * b - 0 + 5 * 7		a * b + 35

Caveats

This technique will not be able to simplify all expressions. For example, these can not be simplified:

(A + 7) / (A + 7)           # should be 1
(A + 7) - (A + 7)           # should be 0
(A + 7) - (7 + A)           # same
(3 + A + 4) - (A + 7)       # same
(A + B + C) - (C + B + A)   # same

To simplify these expressions, more complex algorithms are needed. One step is to normalize the expressions such that different operand orderings can be dealt with. For example, sorting the identifiers in alphabetical order:

(A + C + B)  ==> (A + B + C)
(C + B + A)  ==> (A + B + C)
(B + A + C)  ==> (A + B + C)

The resulting tree:

Then, you'd have to recognize that the entire left subtree of the root is identical to the entire right subtree of the root. You would do this with a recursive algorithm that determines if two trees are identical. The Poor-Man's Way^™ is to simply perform a traversal (pre-, post-, in-order, doesn't matter) and compare the outputs.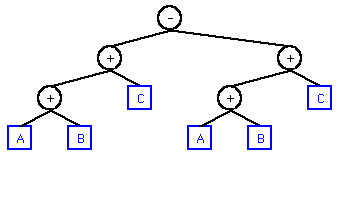

A possibly more elegant solution would be a simple recursive function. Here's a prototype:

// From the example code above  
struct Node
{
  Node *left;
  Node *right;
  int data;
}

bool isIdentical(const Node *left_tree, const Node *right_tree);

And one possible algorithm (psuedocode):

If left_tree is NULL AND right_tree is NULL, return true. (Base case)
If one of the pointers is NULL but the other is not, return false. (Base case. Can't be identical)
Else both pointers are valid.

If data in both pointers is different, return false (Base case. Can't be identical)
Else recursively check the left subtree AND recursively check the right subtree. (Recursive case)

Of course, this is complicated by the fact that different operators have different precedence and commutative properties and you can't ignore that:

(A * C + B)  ==> (A * B + C)  # incorrect
(C - B - A)  ==> (A - B - C)  # incorrect

This requires much more sophisticated logic (in the general case) to make sure that the transformations do not change the underlying meaning. This is non-trivial for dealing with arbitrarily complex expressions.

Self-check Build the parse tree for these expressions:

A + B + C A + B * C A * B + C (A + B) * C A * (B + C)

Substitute integers for A, B, and C and then evaluate the tree using postfix traversal.

Self-check Given the expression tree below, show the postfix expression. Hint: perform a post-order traversal.

Real World: Compilers and Constant Folding

This is how compilers do constant folding. They simply make a tree out of the expression and perform a post-order traversal to evaluate it at compile time.

In the olden days, compilers only did this for literals and compile-time constants because the values had to be known to the compiler. Nowadays, compilers are much smarter and can analyze the code to determine that some variables never change their values.

Given this code (from the link above):

int main()
{
    // a, b, and c are variables, not constants!
  int a = 30;
  int b = 9 - (a / 5); // b is 3
  int c;               

  c = b * 4;           // c is 12
  if (c > 10)          // 12 > 10 (true)
  {
     c = c - 10;       // c is 12 - 10, which is 2
  }

  return c * (60 / a); // return 2 * (60 /30) ==> 2 * 2 ==> 4
}

Compiler-generated assembly code (GNU g++ 5.1):

No optimization	Optimization -O
.file "main.cpp" .text .globl main .type main, @function main: .LFB0: pushq %rbp movq %rsp, %rbp movl $30, -8(%rbp) movl -8(%rbp), %ecx movl $1717986919, %edx movl %ecx, %eax imull %edx sarl %edx movl %ecx, %eax sarl $31, %eax subl %eax, %edx movl %edx, %eax movl $9, %edx subl %eax, %edx movl %edx, %eax movl %eax, -12(%rbp) movl -12(%rbp), %eax sall $2, %eax movl %eax, -4(%rbp) cmpl $10, -4(%rbp) jle .L2 subl $10, -4(%rbp) .L2: movl $60, %eax cltd idivl -8(%rbp) imull -4(%rbp), %eax popq %rbp ret .LFE0: .size main, .-main .ident "GCC: (Mead custom build) 5.1.0" .section .note.GNU-stack,"",@progbits	.file "main.cpp" .text .globl main .type main, @function main: .LFB0: movl $4, %eax ret .LFE0: .size main, .-main .ident "GCC: (Mead custom build) 5.1.0" .section .note.GNU-stack,"",@progbits

No optimization

Optimization -O

  .file "main.cpp"
  .text
  .globl  main
  .type main, @function
main:
.LFB0:
  pushq %rbp
  movq  %rsp, %rbp
  movl  $30, -8(%rbp)
  movl  -8(%rbp), %ecx
  movl  $1717986919, %edx
  movl  %ecx, %eax
  imull %edx
  sarl  %edx
  movl  %ecx, %eax
  sarl  $31, %eax
  subl  %eax, %edx
  movl  %edx, %eax
  movl  $9, %edx
  subl  %eax, %edx
  movl  %edx, %eax
  movl  %eax, -12(%rbp)
  movl  -12(%rbp), %eax
  sall  $2, %eax
  movl  %eax, -4(%rbp)
  cmpl  $10, -4(%rbp)
  jle .L2
  subl  $10, -4(%rbp)
.L2:
  movl  $60, %eax
  cltd
  idivl -8(%rbp)
  imull -4(%rbp), %eax
  popq  %rbp
  ret
.LFE0:
  .size main, .-main
  .ident  "GCC: (Mead custom build) 5.1.0"
  .section  .note.GNU-stack,"",@progbits

  .file "main.cpp"
  .text
  .globl  main
  .type main, @function
main:
.LFB0:
  movl  $4, %eax
  ret
.LFE0:
  .size main, .-main
  .ident  "GCC: (Mead custom build) 5.1.0"
  .section  .note.GNU-stack,"",@progbits

Note that if this is not main but some other function that returns an integer, and the entire body of the function is being reduced to this:

return 4;

The compiler may just remove the call to the function altogether. This means that client code could be reduced from this (assume the function is named foo):

int x = foo();

to this:

int x = 4;

If a, b, and c were declared global instead of local, the compiler won't optimize it. For example:

  // a, b, and c are now global
int a = 30;
int b = 9 - (a / 5); // b is 3
int c;               

int main()
{
  c = b * 4;           // c is 12
  if (c > 10)          // 12 > 10 (true)
  {
     c = c - 10;       // c is 12 - 10, which is 2
  }

  return c * (60 / a); // return 2 * (60 /30) ==> 2 * 2 ==> 4
}

Why might that happen?

If we declare them as static:

  // a, b, and c are now static (file-scope)
static int a = 30;
static int b = 9 - (a / 5);
static int c = b * 4;

int main()
{
  if (c > 10) 
  {
    c = c - 10;
  }

  return c * (60 / a);
}

and compile with -O, we see this (all of the "noise" in the assembly code has been removed and comments added)

main:
  movl  _ZL1c(%rip), %eax   ; put c in eax
  cmpl  $10, %eax           ; compare c with 10
  jle .L2                   ; if less-than or equal, jump to L2
  subl  $10, %eax           ; c is greater than 10, so subtract 10
  movl  %eax, _ZL1c(%rip)   ; put eax back into c
.L2:
  movl  _ZL1c(%rip), %eax   ; put c in eax
  addl  %eax, %eax          ; c + c, same as c * 2
  ret

If we compile with -O2, we see this slightly more optimized version (without the redundant load of c):

main:
.LFB0:
  movl  _ZL1c(%rip), %eax
  cmpl  $10, %eax
  jle .L2
  subl  $10, %eax
  movl  %eax, _ZL1c(%rip)
.L2:
  addl  %eax, %eax
  ret

However, if I add this before main

void foo()
{
  extern int i;
  a = i;
}

All optimizations are removed. But, if I marked foo as static:

static void foo()
{
  extern int i;
  a = i;
}

all optimizations are back on. But, wait, there's more! If I actually call foo:

int main()
{
  foo();
  if (c > 10) 
  {
    c = c - 10;
  }

  return c * (60 / a);
}

all of the optimizations are off again! Aren't modern compilers a Wonderful Thing^™!

Suppose we really didn't want the compiler to optimize the local variables as in the original code. How could we tell the compiler not to optimize the variables a, b, and c? (Obviously, we would just omit the -O2 compiler option, but that will disable ALL optimizations, we just want to disable the ones on the local variables.)

This is the way:

int main()
{
    // a, b, and c will not be optimized
  volatile int a = 30;
  volatile int b = 9 - (a / 5); // b is 3
  volatile int c;               

  c = b * 4;           // c is 12
  if (c > 10)          // 12 > 10 (true)
  {
     c = c - 10;       // c is 12 - 10, which is 2
  }

  return c * (60 / a); // return 2 * (60 /30) ==> 2 * 2 ==> 4
}

This tells the compiler that these variables may be modified outside of the function (not possible, actually!) so leave them alone. No optimizations with those variables will be done.

How about this code?

void foo(int &x); // prototype

int main()
{
  int a = 30;
  int b = 9 - (a / 5); // b is 3
  int c;               

  foo(a);
  foo(b);

    // The code below will not be optimized because
    // foo has indicated it will modify a and b.

  c = b * 4;           // c is 12
  if (c > 10)          // 12 > 10 (true)
  {
     c = c - 10;       // c is 12 - 10, which is 2
  }

  return c * (60 / a); // return 2 * (60 /30) ==> 2 * 2 ==> 4
}

Suprisingly (or maybe not), if the parameter to foo is constant:

void foo(const int &x); // prototype

no optimization takes place. This should give you some insight into how much compilers have improved over the years when it comes to performing deep analysis of the code.

The compilers used are version 5.1 (April 2015) and 5.3 (December 2015). Newer compilers may do even better with the optimizations.