In programming terms, recursion is very much like iteration (looping). In fact, anything you can do iteratively, you can
do recursively.
Recursion is not unique to C++; many languages support it
Basic Idea
- Figure out the pattern of repetition that calls the recursive function. (What is being done repeatedly?)
- Find out what changes in the parameters to cause the problem to
change (get smaller) with each recursive call.
- Figure out the base case or trivial case; this is what stops the recursion.
Example
Printing a string iteratively
First, write down the algorithm in English:
- Start with the first character
- If it's the NUL character, STOP.
- If it's not NUL, print the character
- Move to the next character
- Go to step 2
Another way to write the same algorithm:
- Set the first character as the current character
- While there are more characters in the string
- Print the current character
- Move to the next character
- Go to step 2
The code that implements the algorithm could look like this (assume a valid NUL-terminated string):
void print_string(const char *string)
{
while (*string)
putchar(*string++);
}
What's the complexity of the code above? (Assume N characters in the string. How many characters did
we have to touch?)
Using a for loop:
void print_string(const char *string)
{
int len = strlen(string);
for (int i = 0; i < len; i++)
putchar(string[i]);
}
What's the complexity of the code above? (Assume N characters in the string. How many characters did
we have to touch?)
Using another for loop (as seen in freshmen programming):
void print_string(const char *string)
{
for (int i = 0; i < strlen(string); i++)
putchar(string[i]);
}
What's the complexity of the code above? (Assume N characters in the string. How many characters did
we have to touch?)
Printing a string recursively:
First, write down the algorithm in English:
- If the first character is NUL, STOP.
- Print the first character (head)
- Then print the rest of the string (tail) recursively.
This can be reduced to the statement: "Print the head, and then print the tail recursively."
The head is a single item (no recursion, base case), and the tail is a (smaller) string.
The rest of the string is itself a string, (albeit a shorter one),
and we just stated above how to print a string recursively.
Code to implement the algorithm might look like this:
// Print the first character, and then print the rest ...
void print_string_rec(const char *string)
{
putchar(*string); // Print the first character
print_the_rest(string + 1); // Print the rest of the string
}
Of course, our black box function print_the_rest needs to be implemented at
some point. How do we print the rest of the string? Same as before:
- Print the first character, then
- Print the rest of the string recursively
which leads to:
void print_the_rest(const char *string)
{
putchar(*string); // Print the first character
print_the_rest2(string + 1); // Print the rest of the string
}
and then:
void print_the_rest2(const char *string)
{
putchar(*string); // Print the first character
print_the_rest3(string + 1); // Print the rest of the string
}
void print_the_rest3(const char *string)
{
putchar(*string); // Print the first character
print_the_rest4(string + 1); // Print the rest of the string
}
etc. It's not difficult to see the pattern here and a lot of duplicated functionality
(not to mention the limitation of printing only strings of a certain length). We only
need one version of these identical functions:
void print_the_rest(const char *string)
{
putchar(*string); // Print the first character
print_the_rest(string + 1); // Print the rest recursively
}
But this is still the same functionality as our original print_string_rec function:
void print_string_rec(const char *string)
{
putchar(*string); // Print the first character
print_the_rest(string + 1); // Print the rest of the string
}
So, we can fold all of this functionality into one function:
void print_string_rec(const char *string)
{
putchar(*string); // Print the first character
print_string_rec(string + 1); // Print the rest of the string
}
At this point, we're missing a very crucial piece of code: the terminating condition. (Recursion
is a form of iteration and iterations need to end.)
The terminating condition for printing a string should be when we encounter the NUL character
at the end:
void print_string_rec(const char *string)
{
// If it's the NUL character, do nothing (just return)
if (*string)
{
putchar(*string); // Print the first character
print_string_rec(string + 1); // Print the rest of the string
}
}
This function will handle NUL-terminated strings of any length (including zero-length).
Printing the string magic:
print_string_rec("magic")
putchar("m")
print_string_rec("agic")
putchar("a")
print_string_rec("gic")
putchar("g")
print_string_rec("ic")
putchar("i")
print_string_rec("c")
putchar("c")
print_string_rec("NUL") <---- recursion terminates
Notes:
- Recursion works by applying its algorithm to a smaller version of the problem.
(It should be less work to print the tail of a string than the whole string.)
- Without a terminating condition we will have infinite recursion, which is not unlike
an infinite loop in iteration. Infinite recursion will usually crash the program almost immediately (by
exhausting the stack very quickly).
- There is nothing special or magical about a recursive function. At runtime, it behaves exactly
like any other function, meaning:
- All local variables are re-initialized (or uninitialized) between invocations
- The values of the locals are saved between calls (on the call stack), just as they would be if you called another
function.
- If you need to access previous values of a local variable between calls, you are going to need
to pass the variable to the function as a parameter.
Another recursion example
Printing a string in reverse (iteratively):
Algorithm:
- Set the position to the last character.
- If the current position is less than 0, STOP, else print the character
- Decrement the position.
- Goto 2
void print_string_rev1(const char *string)
{
int len = strlen(string);
for (int i = len; i > 0; i--)
putchar(*(string + i - 1));
}
or
void print_string_rev2(const char *string)
{
int len = strlen(string);
while (len)
{
putchar(*(string + len - 1));
len--;
}
}
Printing a string in reverse (recursively):
Algorithm:
- Print the rest of the string (tail) in reverse.
- Then print the first character (head).
Code:
void print_string_rec_r(const char *string)
{
// If it's the NUL character, do nothing and return
if (*string)
{
print_string_rec_r(string + 1); // Print the rest of the string, recursively
putchar(*string); // Print the head
}
}
Compare this function with the first string-printing function:
void print_string_rec(const char *string)
{
// If it's the NUL character, do nothing and return
if (*string)
{
putchar(*string); // Print the head
print_string_rec(string + 1); // Print the rest of the string, recursively
}
}
Also, compare the iterative version with the recursive version. It is almost impossible to get
the recursive function wrong, whereas, it's very easy to get the iterative version wrong!
Self-check: Implement these recursive functions:
- Write a recursive function to print the values 1 to 10. Here's the prototype: (Call it with a value of 1)
void PrintTen(int value);
- Write a recursive function to print an arbitrary range of numbers. Here's the prototype:
void PrintNumbers(int start, int end);
For example, PrintNumbers(4, 8) will print:
4
5
6
7
8
- Write a recursive function to print the values 10 to 1. (Modify the first function above.)
- Write a recursive function, rec_strlen, to return the string length of a NUL-terminated string.
(Think head and tail with respect to their lengths)
For example, rec_strlen("Hello") will return 5.
Sample solutions
Looking again at the factorial function defined recursively:
N! = N · (N - 1)!
This function assumes that N > 0 and by definition 0! = 1. This function
is recursive because it is defined in terms of itself. The traditional
way of writing recursive definitions is like this:
0! = 1 base case
N! = N · (N - 1)! recursive case
For example, 5! is defined like this:
5! = 5 · 4!
And 4! is defined like this:
4! = 4 · 3!
And so on:
3! = 3 · 2!
2! = 2 · 1!
1! = 1 · 0!
0! = 1 this is the base case
Which ultimately gives us:
5 · 4 · 3 · 2 · 1 · 1 = 120
Sample code
Assembly (Showing the tail recursion removal)
int recursiveFact(int number)
{
if (number == 0)
return 1;
else
return number * recursiveFact(number - 1);
}
Diagram of the recursive function calls:

Another popular function that is defined recursively is the power function:
XN = X · X(N - 1)
This function assumes that N > 0 and by definition X0 = 1.
We would write the recursive definition like this:
X0 = 1 base case
XN = X · X(N - 1) recursive case
Sample code
Find the maximum value in a list of integers recursively.
(Don't use this method in an actual project!)
Base: MaxVal([x]) = x
Recursive:
MaxVal([a1, a2, a3, ..., aN]) = if a1 > MaxVal([a2, ..., aN]) then
a1
else
MaxVal([a2, ..., aN])
Complexities:
- Best case: O(n) (Sorted high to low)
- Worst case: O(2n) (Sorted low to high)
Sample code
Sample code:
int a[] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
int b[] = {10, 9, 8, 7, 6, 5, 4, 3, 2, 1};
int m;
X = 0;
m = RecMaxVal(a, sizeof(a) / sizeof(int));
cout << "RecMaxVal is " << m << ", X = " << X << endl;
X = 0;
m = RecMaxVal(b, sizeof(b) / sizeof(int));
cout << "RecMaxVal is " << m << ", X = " << X << endl;
Output:
RecMaxVal is 10, X = 1023
RecMaxVal is 10, X = 10
Larger test:
int array[32];
for (int i = 0; i < 32; i++)
array[i] = i;
X = 0;
m = RecMaxVal(array, sizeof(array) / sizeof(int));
cout << "RecMaxVal is " << m << ", X = " << X << endl;
Output (after running for about 7 seconds, compiling with -O2)
RecMaxVal is 31, X = 4294967295
Given the 3 functions as defined below:
int f1(int a, int b)
{
int x, y;
x = f2(a);
y = 4 + b;
return x + y;
}
|
int f2(int x)
{
int a, b, c;
a = x;
b = 5;
c = f3(a + b);
return c;
}
|
int f3(int x)
{
int a;
// snapshot taken before
// this line executes:
a = x * 3;
return a;
}
|
What does the following program print?
void main()
{
int x;
float f;
f = 2.7f;
x = f1(2, 3);
cout << x << endl;
}
This image below is a "snapshot" of what the runtime stack (memory) looks like just before
the statement
a = x * 3;
in f3 is executed. (Actually, it's not exactly like than this, but it gets the point across.)
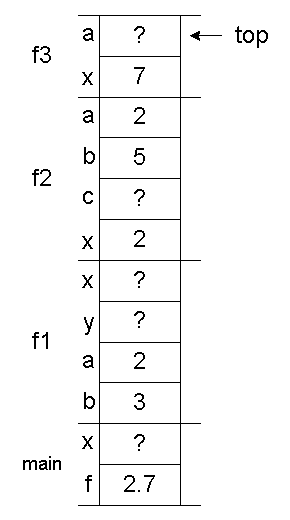
|
int f1(int a, int b)
{
int x, y;
x = f2(a);
y = 4 + b;
return x + y;
}
|
int f2(int x)
{
int a, b, c;
a = x;
b = 5;
c = f3(a + b);
return c;
}
|
int f3(int x)
{
int a;
// snapshot taken before
// this line executes:
a = x * 3;
return a;
}
|
int main()
{
int x;
float f;
f = 2.7f;
x = f1(2, 3);
cout << x << endl;
return 0;
}
|
|
The "stack" and Recursive Programming
- Each function's portion of the stack is called an activation record or
stack frame
- The stack grows and shrinks during program execution.
- This is why local variables are undefined and are called automatic variables
- Global data and dynamically allocated data (and static variables in C++) are not created on
the stack, so they stay around for the life of the program (or until you delete them.)
- Can you see why "infinite recursion" will cause bad things to happen? What thing exactly?
- The runtime stack is what enables recursion to work without any programmer intervention.
It's the LIFO (List In First Out) policy that makes it useful.
Given this recursive definition of Print: (which prints a section of an array)
void Print(const int *list, int first, int last)
{
if (first <= last)
{
cout << list[first] << endl;
Print(list, first + 1, last);
}
}
We can print the second, third, and fourth integers in the array using this syntax:
Print(list, 1, 3)
Self Check:
Write another version to print a "section" of the array. This function should only take 2 parameters:
A pointer to an element in an array and the number of elements to print.
Simulating recursion
Print a range of integers in reverse recursively:
Algorithm:
- Print the rest of the list (tail)
- Print the first value (head)
void PrintRev1(const int *list, int first, int last)
{
if (first <= last)
{
PrintRev1(list, first + 1, last);
cout << list[first] << endl;
}
}
Print a range of integers in reverse iteratively, using an explicit stack:
void PrintRev2(const int *list, int first, int last)
{
// Simulates the runtime stack
std::stack<int> s;
// Simulating the recursive calls
while (first <= last)
s.push(first++);
// Simulating the returns from the recursive calls
while (!s.empty())
{
cout << list[s.top()] << endl;
s.pop();
}
}
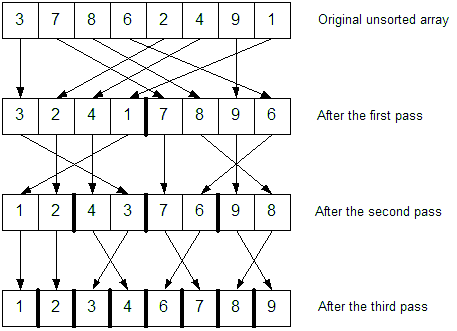
Here's a very simple function that reverses a range of characters in a string iteratively (in place without printing):
void ReverseStringIt(char *s, int from, int to)
{
while (from < to)
{
// Swap the edges first
char c = s[from];
s[from] = s[to];
s[to] = c;
// Advance the "edge pointers"
from++;
to--;
}
}
Simple usage:
char p[] = "123456789";
ReverseStringIt(p, 0, 8); //987654321
ReverseStringIt(p, 0, 3); //432156789
ReverseStringIt(p, 3, 7); //123876549
Implementing a recursive version: How would you state the algorithm in English?
void ReverseStringRec(char *s, int from, int to)
{
if (from < to)
{
// Swap the edges
char c = s[from];
s[from] = s[to];
s[to] = c;
// Reverse the "middle" characters
ReverseStringRec(s, from + 1, to - 1);
}
}
Self Check:
Write a recursive function that can reverse a singly-linked list in-place.
Use the Node struct and function prototype below. (You may want to first try to do this iteratively.)
struct Node
{
Node *next;
int data;
};
void ReverseListRec(Node*& list, Node *prev); // Recursively reverse list in-place
Self Check:
Take any existing linked-list implementation that you've written and rewrite some of the functions to be recursive. (e.g find, free, length, etc.)
Caution: using recursion on a linked-list
is generally not a good idea, especially if the list can be very long as you can run out of stack space.
Here is the code to print out a singly-linked list recursively and in reverse. It is trivial to do so:
void List::PrintListRec(const Node* list) const
{
if (list)
{
std::cout << list->data << " ";
PrintListRec(list->next);
}
}
void List::PrintListRevRec(const Node* list) const
{
if (list)
{
PrintListRevRec(list->next);
std::cout << list->data << " ";
}
}
More linked-list examples.
I hope you can see now why recursion can be a much better solution than iteration in certain
situations. You will do well to familiarize yourself and become comfortable with recursion. Recursion can take a
really ugly solution and turn it into an efficient and elegant solution.
Printing Matrices Recursively
In these examples, each row in the matrix is a recursive call and each column is done iteratively. There
are several ways to accomplish the output. ROWS is 8 and COLUMNS is 8 in all of the examples.
| Code | Output |
|---|
// ROWS in order, COLUMNS in order
void print_matrix1(int row)
{
if (row > ROWS)
return;
// print columns
for (int i = 0; i < COLUMNS; i++)
printf("%4i", row * COLUMNS + i);
printf("\n");
// next row
print_matrix1(row + 1);
}
|
0 1 2 3 4 5 6 7
8 9 10 11 12 13 14 15
16 17 18 19 20 21 22 23
24 25 26 27 28 29 30 31
32 33 34 35 36 37 38 39
40 41 42 43 44 45 46 47
48 49 50 51 52 53 54 55
56 57 58 59 60 61 62 63
64 65 66 67 68 69 70 71
Call:
print_matrix1(0);
|
// ROWS reversed, COLUMNS reversed
void print_matrix2(int row)
{
if (row == 0)
return;
// print columns
for (int i = COLUMNS; i > 0; i--)
printf("%4i", (row - 1) * COLUMNS + i);
printf("\n");
// next row
print_matrix2(row - 1);
}
|
64 63 62 61 60 59 58 57
56 55 54 53 52 51 50 49
48 47 46 45 44 43 42 41
40 39 38 37 36 35 34 33
32 31 30 29 28 27 26 25
24 23 22 21 20 19 18 17
16 15 14 13 12 11 10 9
8 7 6 5 4 3 2 1
Call:
print_matrix2(8);
|
// ROWS reversed, COLUMNS in order
void print_matrix3(int row)
{
if (row > ROWS)
return;
// next row
print_matrix3(row + 1);
// print columns
for (int i = 0; i < COLUMNS; i++)
printf("%4i", row * COLUMNS + i);
printf("\n");
}
|
64 65 66 67 68 69 70 71
56 57 58 59 60 61 62 63
48 49 50 51 52 53 54 55
40 41 42 43 44 45 46 47
32 33 34 35 36 37 38 39
24 25 26 27 28 29 30 31
16 17 18 19 20 21 22 23
8 9 10 11 12 13 14 15
0 1 2 3 4 5 6 7
Call:
print_matrix3(0);
|
// ROWS in order, COLUMNS reversed
void print_matrix4(int row)
{
if (row == 0)
return;
// next row
print_matrix4(row - 1);
// print columns
for (int i = COLUMNS; i > 0; i--)
printf("%4i", (row - 1) * COLUMNS + i);
printf("\n");
}
|
8 7 6 5 4 3 2 1
16 15 14 13 12 11 10 9
24 23 22 21 20 19 18 17
32 31 30 29 28 27 26 25
40 39 38 37 36 35 34 33
48 47 46 45 44 43 42 41
56 55 54 53 52 51 50 49
64 63 62 61 60 59 58 57
Call:
print_matrix4(8);
|
int WIDTH = 8;
int SIZE = 64;
// all recursive
void print_matrix5(int index)
{
if (index >= SIZE)
return;
printf("%4i", index);
// print newline?
if (!((index + 1) % WIDTH))
printf("\n");
print_matrix5(index + 1);
} |
0 1 2 3 4 5 6 7
8 9 10 11 12 13 14 15
16 17 18 19 20 21 22 23
24 25 26 27 28 29 30 31
32 33 34 35 36 37 38 39
40 41 42 43 44 45 46 47
48 49 50 51 52 53 54 55
56 57 58 59 60 61 62 63
Call:
print_matrix5(0);
|
Of course, all of the above could have easily been done using a nested loop
(iteration for rows and columns). These examples demonstrate various ways to
perform iteration using recursion instead.
For all values of n > 1, we have the Fibonacci numbers defined recursively as:
F0 = 0 base case
F1 = 1 base case
FN = Fn-1 + Fn-2 recursive case
So the first 10 Fibonacci numbers are: 0, 1, 1, 2, 3, 5, 8, 13, 21, and 34.
Implementing this iteratively causes the "elegance" to get lost. What does Foo do?
int IterFibonacci(int number)
{
if (number == 0)
return 0;
else if (number == 1)
return 1;
else
{
int v1 = 1, v2 = 0;
for (int i = 2; i <= number; i++)
{
int temp = v1;
v1 += v2;
v2 = temp;
}
return v1;
}
}
|
int Foo(int X)
{
if (X == 0)
return 0;
else if (X == 1)
return 1;
else
{
int v1 = 1, v2 = 0;
for (int i = 2; i <= X; i++)
{
int temp = v1;
v1 += v2;
v2 = temp;
}
return v1;
}
}
|
How many times does the for loop iterate? What is the complexity?
Now, implementing it recursively from the definition is trivial and almost writes itself:
int RecFibonacci(int number)
{
if (number == 0) // Base case: F0 = 0
return 0;
else if (number == 1) // Base case: F1 = 1
return 1;
else // Recursive case: FN = FN-1 + FN-2
return RecFibonacci(number - 1) + RecFibonacci(number - 2);
}
How many times is the function called for a given number?
To help you really see how bad this is, we can build the execution tree:
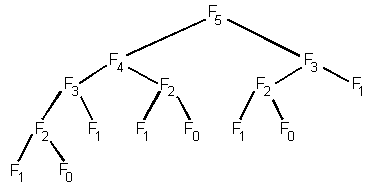
The parent/child relationship has the meaning:
"To calculate the parent, we have to calculate the children first."
So, to compute F5, we need to first compute F4 and F3. But,
in order to compute F4, we need to compute F3 and F2, etc.
This table shows the number of times the RecFibonacci function is called for each value:
Number F0 F1 F2 F3 F4 F5 F6 F7 F8 F9
Value 0 1 1 2 3 5 8 13 21 34
Calls 1 1 3 5 9 15 25 41 67 109
For example, the number of calls to RecFibonacci to evaluate F7 is
41. This is because it evaluates F6 (25 calls) and F5 (15 calls)
plus the original call for F7.
So, the number of calls to evaluate FN is F(N - 1) + F(N - 2) + 1
This is roughly on the order of 2N, which as we know is very, very bad.
Notes
- The "problem" with the recursive version is that later calculations depend on the earlier ones, and these were discarded.
- The iterative version saves and uses those previously-calculated values.
- This "saving of previously calculated values" is termed dynamic programming
or memoization. (That's spelled correctly!)
- When the smaller (sub-problems) of the original problem are not independent problems, (i.e. they depend on each other),
the resulting algorithm can perform poorly.
- Naive recursive implementations (like the one above) can lead to a lot redundant computations. We first saw that here.
Self-check Modify the recursive Fibonacci implementation above to improve it (it should be O(N)).
The key to solving this is to recognize what (discarded) calculations must be passed to the next call of the function.
The goal behind the problem is to place 8 queens on a chessboard so that no queen threatens another.
Another way to state this (for those not familiar with the capabilities of the queen in chess) is to
place 8 markers on a standard 8x8 chess board so that no two markers are on the same line vertically,
horizontally, or diagonally.
| Queen's movements | | A solution |
|---|

|
|

|
- There are many solutions (arrangements of queens) that satisfy the criteria mentioned above.
- As it turns out, a recursive solution is the simplest to implement (but not necessarily the fastest).
- The implementation will involve a technique called backtracking.
- Backtracking is a popular technique that computers use to solve problems by systematically evaluating all possible solutions.
- Incidentally, exhaustive backtracking is one way in which
a maze can be solved.
The algorithm is fairly trivial and is best demonstrated graphically with this application: (generalized for an NxN board)
N-Queens Test Application
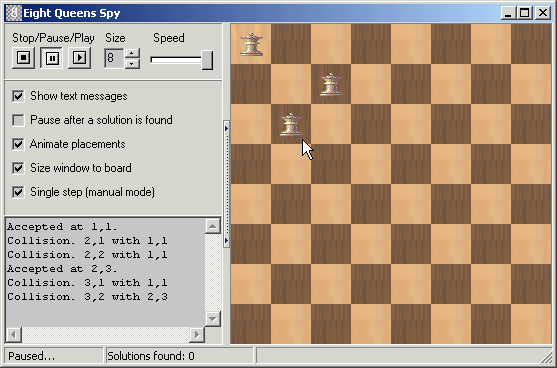
Number of solutions for boards of size:
Solutions for 1 x 1: 1
Solutions for 2 x 2: 0
Solutions for 3 x 3: 0
Solutions for 4 x 4: 2
Solutions for 5 x 5: 10
Solutions for 6 x 6: 4
Solutions for 7 x 7: 40
Solutions for 8 x 8: 92
Solutions for 9 x 9: 352
Solutions for 10 x 10: 724
Solutions for 11 x 11: 2,680
Solutions for 12 x 12: 14,200
Solutions for 13 x 13: 73,712
Solutions for 14 x 14: 365,596
Solutions for 15 x 15: 2,279,184
Solutions for 16 x 16: 14,772,512
Solutions for 17 x 17: 95,815,104
Solutions for 18 x 18: 666,090,624
Pseudo-code for a recursive implementation:
bool board[8][8];
int solutions = 0;
int Solve()
{
// Initialize all squares to empty
// Call PlaceQueen with row 0 to start the search
PlaceQueen(0);
// Return number of solutions
}
void PlaceQueen(int row)
{
// Put a queen in the specified row, starting at the first column
for(int column = 0; column < 8; column++)
{
board[row][column] = true;
// Call Threatened to determine if placement was valid
// (may have to remove it and try another column or go back to previous row)
// Call PlaceQueen recursively to place queens in subsequent rows
// until a queen is successfully place in last row, or all rows/columns
// have been attempted
}
}
int Threatened(int row, int column)
{
// Determine if there is a collision with any other queen
// (vertically, horizontally, and diagonally)
// If there is a collision, return TRUE, otherwise return FALSE
}
A client would simply do this:
int solutions = Solve(); // Returns the number of solutions
Another version of this uses rooks instead of queens: (Download)
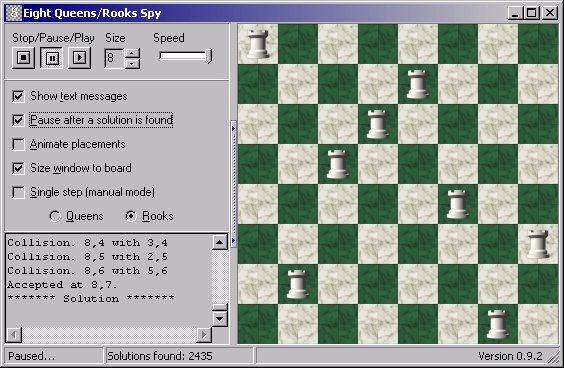
Number of solutions for boards of size:
Solutions for 1 x 1: 1
Solutions for 2 x 2: 2
Solutions for 3 x 3: 6
Solutions for 4 x 4: 24
Solutions for 5 x 5: 120
Solutions for 6 x 6: 720
Solutions for 7 x 7: 5040
Solutions for 8 x 8: 40320
It's just the factorial of the board size.
Yet-another chess-related recursive algorithm is "The Knight's Tour":
| Valid moves for the knight | | A demo program |
|---|
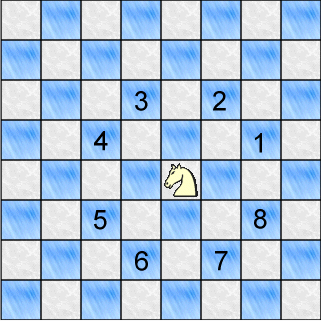
|
|
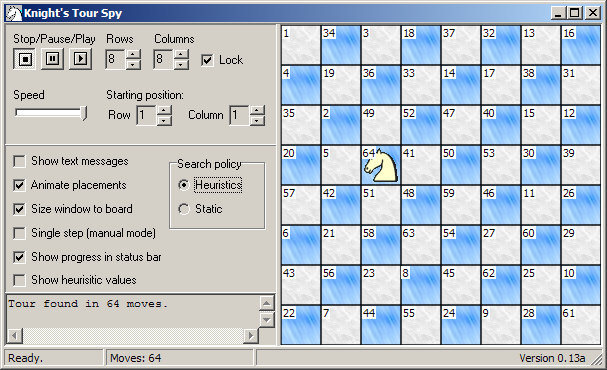
|
Download/run the demo program.
A Direct 3D version of a driver for the 8-Queens algorithm.
Several years ago, a Digipen student (John Lykins)
took his 8-Queens implementation and created a 3D driver for it:
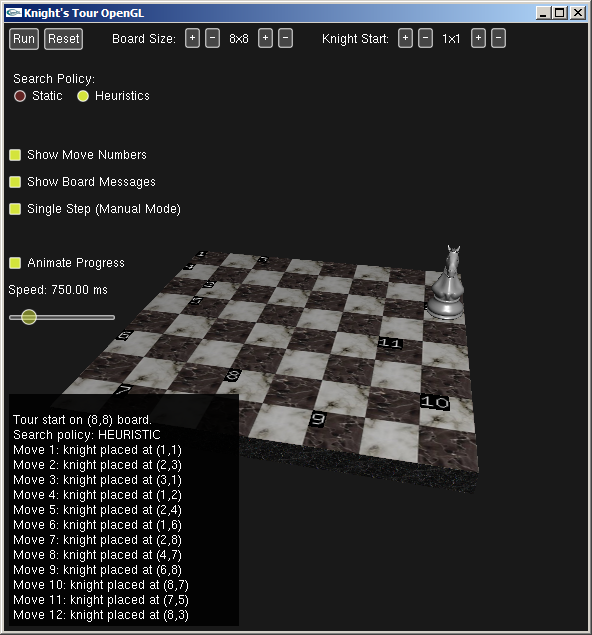
An OpenGL version of the driver for the Knight's Tour algorithm.
Several years ago a Digipen student (Nathan Williams) created an OpenGL version
of the driver for his Knight's Tour implementation.