Abstract Data Types
All computer systems are based on layers of abstraction
- As programmers, we typically consider the bit level, 0 and 1, as the lowest level
- Hardware engineers actually go down to the electron level
- We talk about a sequence of 8 bits as a byte, representing any of 256 "values"
- 01000001 is the character 'A'
- 01000001 is the integer 65
- A larger sequence of bits (or bytes) can instruct the computer to do things
- 01001101001010010010100101010001110 might cause the CPU to store the value 65 in some register
- This sequence may have an abstract representation as MOV AX, 65
- An even larger sequence can implement a larger instruction or an entire program
Programming languages are abstractions
- A CPU only "speaks" its native language, usually assembly language (abstraction).
- Higher-level languages (e.g BASIC, C, C++, C#, Java, Pascal, Python, Rust) are another level of abstraction.
- Languages that can translate into ASM are essentially equivalent in capability.
- One reason, then, for the multitude of languages is in the effort required by the
programmer to express the solution.
- Also, the quality of the resulting translated code is of concern in the real world,
although not necessarily related to the source language.
High-level languages came about by identifying the necessary constructs (abstractions):
- load/store (assignment, read/write memory)
- arithmetic (add, subtract, multiply, divide)
- decisions (conditionals)
- repetition (loops)
- sub-programs (function calls)
These are the basic building-blocks of all programs.
From the Sedgewick book:
An abstract data type (ADT) is a data type (a set of values and a collection of operations on those values)
that is accessed only through an interface. We refer to a program that uses an ADT as a client, and
a program that specifies the data type as an implementation.
- Clients can only access the ADT through the interface (public methods in C++)
- The interface is opaque. (e.g. Handles (pointers to pointers) are considered opaque)
- C++ is a hybrid in that the internal private data types are visible (to the programmer) but are not
accessible from client code.
Why use an ADT?
- Can implement the functionality in different ways (memory use vs. speed) without changing client code.
- Don't have to recompile the client code (may have to re-link the code)
- Supports code reuse and modular programming
- Can limit the size and complexity for a given solution
- Easier to test localized functionality with driver programs
A linked list abstraction using an array to implement a linked list. The client
has no knowledge of the underlying data structures.
- In addition to an ADT itself, we are interested in collections of ADTs.
- The algorithms we study are particularly geared towards collections.
- A collection is also an ADT.
- We manipulate the collection using a public interface, just like a "simple" ADT.
- Unlike a simple ADT (which is generally unique), collections have a common interface
- Adding or Inserting an item (front, back, middle)
- Removing an item
- Counting the number of items
- Searching the items (traversing)
- Sorting the items
- Performing some operation on all of the data (think functors)
Once we have the fundamental operations implemented, we can create specific ADTs (concrete types)
from the more general ADT.
Pushdown Stack ADT
From the book:
A pushdown stack is an ADT that comprises two basic operations: Insert (push) a new item, and
remove (pop) the item that was most recently inserted.
The stack is a LIFO (last-in, first-out) paradigm.
Q: What data structure employs the FIFO (first-in, first-out) paradigm?
A: a queue
The interface to our stack looks like this:
Stack1(int capacity) // constructor
void Push(char item) // add an item to the top
char Pop() // remove the top item
bool IsEmpty() // check if empty
Our first implementation (array) of a Stack: (notice the capacity in the constructor)
class Stack1
{
private:
char *items;
int size;
public:
Stack1(int capacity)
{
items = new char[capacity];
size = 0;
}
~Stack1()
{
delete[] items;
}
void Push(char item)
{
items[size++] = item;
}
char Pop()
{
return items[--size];
}
bool IsEmpty()
{
return (size == 0);
}
};
Using the first Stack class:
int main()
{
const int SIZE = 10;
Stack1 stack(SIZE);
char *p = "ABCDEFG";
for (unsigned int i = 0; i < strlen(p); i++)
stack.Push(p[i]);
while (!stack.IsEmpty())
cout << stack.Pop();
cout << endl;
return 0;
}
The output:
GFEDCBA
There are some limitations of this Stack class:
- Only accepts char type. (Can use C++ template classes)
- No error checking (e.g. Stack may be empty when calling Pop method.)
- Size is kind of hard-coded (can't grow the Stack if we need more space, could be wasted unused space.)
- Complexity of push and pop?
- Suppose we wanted to grow and/or shrink the data. What is the complexity?
A second (linked-list) version of the Stack class will require a Node structure of some sort:
struct CharItem
{
CharItem *next;
char data;
};
The second implementation of a Stack class:
class Stack2
{
private:
CharItem *head;
int size;
int capacity;
public:
Stack2(int capacity)
{
head = 0;
this->capacity = capacity;
size = 0;
}
~Stack2()
{
while (head)
{
CharItem *t = head->next;
Free(head);
head = t;
}
}
void Push(char c)
{
if (size >= capacity)
return;
CharItem *item = Allocate();
item->data = c;
item->next = head;
head = item;
size++;
}
char Pop()
{
char c = head->data;
CharItem *temp = head;
head = head->next;
Free(temp);
return c;
}
bool IsEmpty()
{
return (head == 0);
}
};
In this implementation:
- The client code doesn't change at all. (Stack abstraction)
- There really is no limit to the size
- The class includes a capacity field to detect a "full" stack
- Complexity of push and pop? Complexity of growing the stack?
Complexity of the destructor?
- The class uses the generic Allocate and Free routines
Here's an implementation of the generic allocation/deallocation that do nothing special.
You can easily replace these with your own memory manager.
CharItem *Allocate()
{
return new CharItem;
}
void Free(CharItem *item)
{
delete item;
}
We still have some limitations:
- Still only accepts char type.
- No error checking (e.g. Stack may be empty when calling Pop method.)
- With small data there can be significant overhead.
- However, there is no real size limit at all and we don't waste any space.
A third version (array) using a
template class: (almost identical to the first implementation)
template <typename Item>
class Stack3
{
private:
Item *items;
int size;
public:
Stack3(int capacity)
{
items = new Item[capacity];
size = 0;
}
~Stack3()
{
delete[] items;
}
void Push(Item item)
{
items[size++] = item;
}
Item Pop()
{
return items[--size];
}
bool IsEmpty()
{
return (size == 0);
}
};
|
|
class Stack1
{
private:
char *items;
int size;
public:
Stack1(int capacity)
{
items = new char[capacity];
size = 0;
}
~Stack1()
{
delete[] items;
}
void Push(char item)
{
items[size++] = item;
}
char Pop()
{
return items[--size];
}
bool IsEmpty()
{
return (size == 0);
}
};
|
Client code is
almost identical:
int main()
{
const int SIZE = 10;
Stack3<char> stack(SIZE); // This is the only change
char *p = "ABCDEFG";
for (unsigned int i = 0; i < strlen(p); i++)
stack.Push(p[i]);
while (!stack.IsEmpty())
cout << stack.Pop();
cout << endl;
return 0;
}
The output:
GFEDCBA
An advantage of this implementation:
|
int main()
{
const int SIZE = 5;
Stack3<int> stack(SIZE);
for (unsigned int i = 1; i <= SIZE; i++)
{
cout << 1000 * i << endl;
stack.Push(1000 * i);
}
cout << endl;
while (!stack.IsEmpty())
cout << stack.Pop() << endl;
return 0;
}
|
The output:
1000
2000
3000
4000
5000
5000
4000
3000
2000
1000
|
In this implementation:
- The client code changes only slightly (but only once and it's simple)
- Still no error checking.
- It's still an array, so we have pros/cons of that data type (complexity, growth).
- Accepts any data type (almost).
- Templates in C++ can potentially generate a lot of code.
A fourth implementation using linked-lists of generic pointers.
We use this Node structure:
struct Item
{
Item *next;
void *data;
};
- Similar to the second version, change CharItem to Item (generic)
- The data is untyped (void *)
- Many frameworks are implemented this way.
- Simpler than a template class (not C++ specific) with possibly less memory requirements, but not as safe.
- Many languages have pointers, very few have generic programming (templates in C++.)
The interface/implementation:
class Stack4
{
private:
Item *head;
int size;
int capacity;
public:
Stack4(int capacity)
{
head = 0;
size = 0;
this->capacity = capacity;
}
~Stack4()
{
// walk the list and delete each item
while (head)
{
Item *t = head->next;
Free(head);
head = t;
}
}
void Push(void *data)
{
if (size >= capacity) // stack is full
return; // do nothing
Item *item = Allocate();// allocate new item
item->data = data; // insert new item at head
item->next = head;
head = item;
size++;
}
void *Pop()
{
void *p = head->data; // get top item
Item *temp = head; // update head
head = head->next;
Free(temp); // deallocate
return p;
}
bool IsEmpty()
{
return (head == 0);
}
};
Client using the fourth implementation:
int main()
{
const int SIZE = 10;
Stack4 stack(SIZE);
char *p = "ABCDEFG";
for (unsigned int i = 0; i < strlen(p); i++)
stack.Push(&p[i]); // push address of data;
while (!stack.IsEmpty())
{
char *c = (char *) stack.Pop();
cout << *c; // dereference data;
}
cout << endl;
return 0;
}
The output:
GFEDCBA
A less trivial example:
struct TStudent
{
float GPA;
int ID;
int Year;
};
int main()
{
const int SIZE = 5;
Stack4 stack(SIZE);
for (int i = 0; i < SIZE; i++)
{
TStudent *ps = new TStudent;
ps->GPA = GetRandom(100, 400) / 100.0;
ps->ID = GetRandom(1, 1000);
ps->Year = GetRandom(1, 4);
cout << "Student ID: " << ps->ID << ", Year: " << ps->Year << ", GPA: " << ps->GPA << endl;
stack.Push(ps);
}
cout << endl;
while (!stack.IsEmpty())
{
TStudent *ps = (TStudent *) stack.Pop();
cout << "Student ID: " << ps->ID << ", Year: " << ps->Year << ", GPA: " << ps->GPA << endl;
}
return 0;
}
The output:
Student ID: 468, Year: 3, GPA: 1.41
Student ID: 170, Year: 1, GPA: 1.12
Student ID: 359, Year: 3, GPA: 1.4
Student ID: 706, Year: 2, GPA: 1.83
Student ID: 828, Year: 2, GPA: 2.04
Student ID: 828, Year: 2, GPA: 2.04
Student ID: 706, Year: 2, GPA: 1.83
Student ID: 359, Year: 3, GPA: 1.4
Student ID: 170, Year: 1, GPA: 1.12
Student ID: 468, Year: 3, GPA: 1.41
Considerations with this implementation:
- The implementation is simple and will deal with any (pointer) data.
- The overhead may be significant, but can be memory efficient if implemented as an array (memory manager).
- The memory usage of the stack is independent of the size of the data (always sizeof(void *)).
- This class is not as type-safe as a template class.
- The client will always interact in the same way, that is, pushing addresses.
- Arithmetic expressions usually use infix notation: the operator is between the operands (3 + 4).
- Postfix notation has the operators after the operands: (3 4 +).
This is also called RPN for Reverse Polish Notation.
Many calculators were made this way.
- Postfix has the nice property that there is no ambiguity; you don't need parentheses:
- Infix, with parens: 5 * ( ( ( 9 + 8 ) * ( 4 * 6 ) ) + 7) = 2075
- Infix, no parens: 5 * 9 + 8 * 4 * 6 + 7 = 244
- Postfix: 5 9 8 + 4 6 * * 7 + * = 2075
- Infix, with parens: 5 * 9 + ( 8 * 4 ) * ( 6 + 7 ) = 461
- Postfix: 5 9 * 8 4 * 6 7 + * + = 461
A stack is the perfect data structure to implement this paradigm. Suppose we have a stream of tokens: (24 x 17 = 408)
5 9 8 + 4 6 * * 7 + *
and we want to evaluate it. The algorithm is as follows:
- When we see an operand, we push it on the stack
- When we see an operator we:
- pop the top 2 items (operands)
- perform the arithmetic:
operand1 operator operand2
- push the result of the arithmetic
- When we have no more tokens, the answer is on the top of the stack (It will be the only item on the stack.)
Self-check Evaluate the expression: 5 9 8 + 4 6 * * 7 + * using a stack where you
push and pop from the top.
A very simple Evaluate function: (Supports only single-digits for input)
// postfix is something like: "598+46**7+*"
int Evaluate(const char *postfix)
{
Stack1 stack(strlen(postfix));
while (*postfix)
{
char token = *postfix;
if (token == '+')
stack.Push(stack.Pop() + stack.Pop());
else if (token == '*')
stack.Push(stack.Pop() * stack.Pop());
else if (token >= '0' && token <= '9')
stack.Push(token - '0');
postfix++;
}
return stack.Pop();
}
Client code:
int main()
{
char *postfix = "598+46**7+*";
cout << postfix << " = " << Evaluate(postfix) << endl;
return 0;
}
Some examples:
598+46**7+* = 2075
34+ = 7
34+7* = 49
12*3*4*5*6* = 720
Self-check Modify the Evaluate function above to support subtraction and division as well. (Note: You'll
need to pay attention to the order of operands.) Try it with
"2 * 8 / 4 + 5 * 6 - 8" which is "2 8 * 4 / 5 6 * + 8 -" in postfix.
Converting Infix to Postfix
Input: An infix expression.
Output: A postfix expression.
Examples from above:
- Infix, with parens: 5 * ( ( ( 9 + 8 ) * ( 4 * 6 ) ) + 7) = 2075
- Postfix: 5 9 8 + 4 6 * * 7 + * = 2075
- Infix, with parens: 5 * 9 + ( 8 * 4 ) * ( 6 + 7 ) = 461
- Postfix: 5 9 * 8 4 * 6 7 + * + = 461
- Infix: 2 * 5 * 2 * 8 + 4 + 5 + 3 = 172
- Postfix: 2 5 2 8 * * * 4 + 5 + 3 + = 172
The algorithm is as follows: Scan the input expression from left to right until there are no more symbols. Depending on what the symbol is,
you need to perform these actions:
- Operand - send to the output
- Left parenthesis - push onto the stack
- Right parenthesis - operators are popped off the stack and sent to the output until a left parenthesis is found (and then discarded).
- Operator
- If the stack is empty, push the operator.
- If the top of the stack is a left parenthesis, push the operator onto the stack.
- If the top of the stack is an operator which has the same or lower precedence than the scanned operator,
push the scanned operator.
- If the top of the stack is an operator which has higher precedence, pop the stack and send to
the output. Repeat the algorithm with the new top of stack.
- If the input stream is empty and there are still operators on the stack, pop all of them and add them to the output.
Note that the only symbols that exist on the stack are operators and left parentheses. Operands and right parentheses are
never pushed onto the stack.
Self-check - Implement a function that converts an infix expression into a postfix expression. (Hint: You will want
to use a stack class. Duh.) Use your implementation to convert this infix expression to postfix:
(7 + 5) * (3 + 4) - (4 * (9 - 2))
- The interface is identical, the implementations are not.
- What is the worst case time complexity for:
- A Push operation with an array? A Pop?
- A Push operation with a linked-list? A Pop?
- How does the complexity change if the details of the implementation change (not just the structure)?
- Manipulate front of an array.
- Manipulate back of single-linked list.
- What about memory requirements?
- Scalability? Access times? (Complexity amortization)
- Implementation complexity? (Often ignored in abstract analysis)
- Hardware architectures? (cache, locality of reference)
Similar to stacks, but more general:
- We usually mean a FIFO queue (First-In, First-Out).
- Add an item to the front and remove an item from the back.
- There are other policies for other queues:
- Add to either end, remove from either end
- Add to either end, remove random element
- Add to either end, remove from anywhere (depending on criteria)
- Ignore/replace duplicates (potentially expensive)
Implementing Queues:
- Arrays can be expensive to remove from the front. O(n)
- Use a circular array. O(1)
- Linked lists can be expensive to add to end. O(n)
- Use a tail pointer. O(1)
- Double-linked list for removing from the end. O(1)
- Cost for removing from the end of a single-linked list?
- Selecting item to remove based on criteria may require some kind of sorting.
- The time to add and remove items may be different.
- Sorted vs. unsorted, array vs. linked list affect the time.
- Implementing a FIFO Queue as a linked-list is straight-forward.
- Implementing it using an array (efficiently) is slightly more interesting.
Self-check Evaluate the expression: 5 9 8 + 4 6 * * 7 + * using a queue
(instead of a stack like above) where
you add to the back, but remove from the front.
We will use a circular array of SIZE elements
- We can't assume the array is indexed from 0 to SIZE - 1. (C/C++ assumes this about arrays)
- We have to keep track of the start and end of the array (other languages do this all the time).
- Need to handle "running off" the end; we'll "wrap" around to "grow" the array.
- If tail == head, the queue is empty.
- If (tail + 1) % SIZE == head, the queue is full. (Accounts for wrapping around.)
- Number of items in queue is (tail - head + SIZE) % SIZE.
- We keep one unused slot to distinguish between full and empty.
- A circular array gives us O(1) for both adding and removing.
The Queue after construction and adding 3 items: (Note that the shaded blocks indicate unused slots in the
Queue)
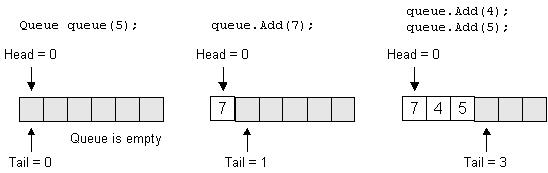
Removing one item, adding 3, then removing 4 more:
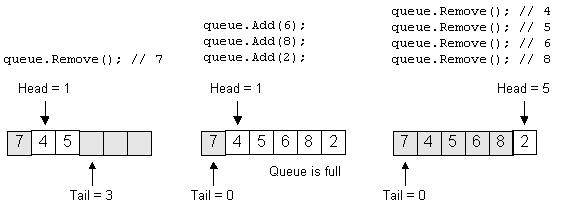
Adding until full, removing until empty:
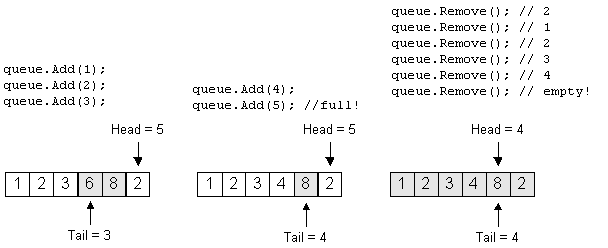
The implementation is left as an exercise for the student.
Self-check Using the class interface below, implement the Queue as a circular array.
class Queue
{
public:
Queue(int MaxItems);
~Queue();
void Add(int Item); // Push
int Remove(); // Pop
bool IsFull() const;
bool IsEmpty() const;
};
- Queues and Stacks can be implemented using arrays or linked lists
- The interface is essentially the same as a Stack. (Many implementations use the names
Push and Pop.)
- Depending on how you implement them changes the complexity from O(n) to O(1)
- Each have trade-offs (time vs. space)
- What about a sorted Stack/Queue?
- Which is the best ADT to use? (Hint: What is the best programming language?)
Here's a C++ class for an abstract interface of a PriorityQueue:
class PriorityQueue
{
private:
// private data
public:
PriorityQueue(int capacity);
~PriorityQueue();
void Add(int Item);
int Remove();
bool IsEmpty() const;
bool IsFull() const;
void Dump() const;
};
We could implement this with either a linked list or an array. Only the private data would change.
| Linked list | | Array |
|---|
struct PQNode
{
PQNode *next;
int data;
};
class PQList
{
private:
PQNode *list_;
int capacity_;
int count_;
public:
// public interface (same as the array)
};
|
|
class PQArray
{
private:
int *array_;
int capacity_;
int count_;
public:
// public interface (same as the list)
};
|
However, the complexity of the algorithms depends on how the list/array is implemented. (Sorted vs. unsorted).
- What is the policy chosen for adding and removing elements?
- Which of the two implementations has a more efficient Add method? Why?
- Which of the two implementations has a more efficient Remove method? Why?
- The sort order doesn't matter because the client isn't expecting any kind of ordering.
- The client can put items into the container in any order, but will always expect
the largest (or smallest) item to be removed.
Here's a sample application using the Priority Queue. (Assume that PQList keeps the list sorted.)
And the associated output:
8 7 5 4 2 1
Removing: 8
7 5 4 2 1
Removing: 7
5 4 2 1
Removing: 5
4 2 1
If we replace this line:
PQList pq(10); // Sorted linked list implementation
with this one:
PQArray pq(10); // Array implementation (assume unsorted array)
still inserting the items in the same order as before:
pq.Add(4); pq.Add(7); pq.Add(2);
pq.Add(5); pq.Add(8); pq.Add(1);
we get this:
4 7 2 5 8 1
Removing: 8
4 7 2 5 1
Removing: 7
4 1 2 5
Removing: 5
4 1 2
The result is the same, but the implementations (and complexities) are different.
Self-check Using the class interface above, implement two priority queues. One
using an array and one using a linked list. You can decide whether or not to keep
it sorted.
What is the complexity when adding items to the queue when implemented as an unsorted array? Sorted array?
What is the complexity when adding items to the queue when implemented as an unsorted linked-list? Sorted List?
What is the complexity when removing items from the queue when implemented as an unsorted array? Sorted array?
What is the complexity when removing items from the queue when implemented as an unsorted linked-list? Sorted List?
Realize that adding and removing requires two actions. The first is locating the item.



